How to Speed Up Your AB Test
Part 1: Measure Twice, Cut Once
Part 1: Measure Twice, Cut Once
This post was first published on The Craft, Faire’s technical blog. It is the first in our multi-part series on accelerating decision-making using A/B Testing.
Like many hypergrowth startups, Faire uses experimentation to quickly iterate on our product and make better decisions. However, unlike many of our peers that serve consumer markets of hundreds of millions or even billions of potential users, our marketplace is built for small businesses, of which there are roughly 30 million in the United States [0]. Coupled with the fact we are barely three years old, this means that sample sizes for our experiments tend to be smaller than data science teams at other tech companies have the luxury of experimenting with. As a case in point, our platform currently serves on the order of 100,000 retailers and 10,000 makers.
Smaller samples might not be a problem when a team is testing effect sizes that are relatively large. But in our case, many of the easy product wins have already been realized and we have to run a larger volume of experiments to find the really big lifts (a topic we plan to write more on soon.) Due to these constraints, we often found ourselves being asked by Product Managers why their experiments were taking so long to reach significance or what they can do to speed them up. In response to these requests, we built the first version of tools to accelerate our experimental results and developed guidelines for Data Scientists, Engineers, and Product Managers designing experiments to ensure that we can reach decisions sooner and with higher confidence in our conclusions.
In this series of posts, we provide an overview of the various techniques that we currently employ in the service of speeding up our AB tests, some simple and others more technical in nature. The accompanying Python notebook provides examples and working code to concretely demonstrate the impact of these techniques and provide you with a starting point for improvements you might make to your own experimentation program.
Experimental Design
Taking the time upfront to design experiments that will yield the most useful results as soon as possible is an effective way to ensure that teams don’t waste time on tests that answer the wrong questions or take too long to answer the right ones. Furthermore, documenting experiments in a systematized way makes it harder for companies to forget or misremember the results of prior tests [1]. This is especially important for experiments with non-intuitive results and those that don’t generalize to your entire population of users. And having this repository of historical data allows teams to develop better prior beliefs around what kind of product treatments do and do not work, on what segments of the user base, which metrics they move, and by how much.
Better Metrics
When designing experiments at Faire, one of the first decisions we make is what the primary metric will be. There are a number of tradeoffs we usually have to make to find a metric that both captures the behavior that we are trying to affect with our treatment and that we anticipate will converge quickly enough to give us a statistically significant result. The two dimensions that are most important are the proximity of the metric to the treatment (as a proxy for effect size) and the expected variance of the metric.
Proximity
Because we have an order of magnitude more retailers than makers, most of our experiments are run on the demand side of our marketplace. In the case of retailers, the metrics that PMs would like to measure most of the time are related to Gross Merchandise Value (GMV) as increasing it reflects retailers getting more economic value from the product and it is one of our key business metrics. This can be challenging in practice as GMV is downstream from everything that we test. For example, changes that we make to our signup flow are removed from the retailer actually placing an order by many intermediate steps. Therefore, any lift we see in the number of signups will often be significantly reduced by the point in the customer journey that a retailer places an order.
We can highlight this with a simple example in which we bucket visitors who then make their way through a conversion funnel by signing up, adding to cart, and placing an order. In this example, we observe a large lift in conversion from visit to sign up and assume no difference in conversion for adding to cart and ordering.
For the sake of simplicity, we run Chi-square tests for the hypotheses that the conversion rates differ between treatment and control at each step in the funnel. We see significant results for signup and add to cart conversion but not for order conversion. This is driven by the fact that the absolute lift declines as we move down the funnel, while the variance of the conversion increase as the values approach zero.
print(proportion.proportions_chisquare(summary_treatment_1['signed_up'], summary_treatment_1['count'])[1])print(proportion.proportions_chisquare(summary_treatment_1['added_to_cart'], summary_treatment_1['count'])[1])print(proportion.proportions_chisquare(summary_treatment_1['ordered'], summary_treatment_1['count'])[1])4.826037697355727e-060.00274199063336884620.11399561233236452The general solution to this issue is to choose a primary metric that is proximate to the change we make in the product. In this case, the obvious choice would be the conversion from visiting to signing up. However, we wouldn’t be sure that any additional signups resulting from our treatment actually end up engaging in the downstream behaviors that we ultimately want to drive, such as placing orders. Two ways that we mitigate this are by choosing appropriate secondary metrics (add to cart and order conversion would be good candidates in this case) as well as leveraging our repositories of previous experiments and observational studies to develop prior beliefs around the strength of the relationship between lifts in our primary metric and those downstream from it. In short, if we have reason to believe that a lift in sign-ups translates to a lift in orders then we don’t necessarily need to wait for our order conversion lift to reach significance (but don’t conclude there is no change in a secondary metric with an underpowered test [2].) Finally, in the case that we lift signup conversion but not the downstream metrics, future experiments on signups will still benefit from increased sample sizes, thereby allowing us to bootstrap our way to more significant results over time.
Variance
The second factor to take into consideration when choosing metrics is their expected variance relative to their expected effect size. For example, proportion metrics (those where the numerator is a subset of the denominator) such as signup conversion or the percent of retailers visiting a brand are bounded between 0 and 1 and produce estimates with lower errors than those of unbounded metrics.
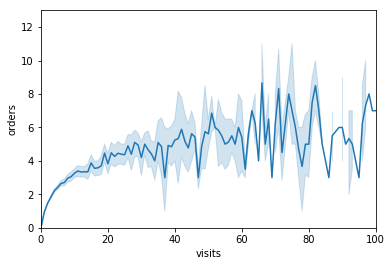
Choosing proportion metrics over unbounded metrics such as GMV per retailer is a common way for us to reduce the time it takes for an experiment to reach a significant result. But within the set of available mathematically unbounded metrics, some are “more unbounded” than others in reality. In the case of retailers on Faire, they are effectively unconstrained in the number of times they can visit maker pages on the site, while their ability to place orders with us is constrained by the amount of inventory they can sell through their stores. This means that the distribution of orders per retailer typically has a much lower variance than that of brand visits per retailer.
To illustrate this we construct a hypothetical experiment in which the expected number of orders is logarithmically related to the number of brand visits. This type of relationship is not uncommon as it reflects the fact that digital behavior is effectively unconstrained while financial budgets in the real world most certainly are. We further assume that both visits and orders are lifted by 5% in the treatment. Again, running t-tests comparing the two samples for visits and orders shows that we’d recognize a significant result for the latter due to it having lower variance in relation to its mean as compared to the former.
print(stats.ttest_ind(experiment_2['visits'][experiment_2['treatment'] == 1], experiment_2['visits'][experiment_2['treatment'] == 0]))print(stats.ttest_ind(experiment_2['orders'][experiment_2['treatment'] == 1], experiment_2['orders'][experiment_2['treatment'] == 0]))Ttest_indResult(statistic=0.7573654245170063, pvalue=0.44884881305779467)Ttest_indResult(statistic=2.5239860524427873, pvalue=0.011618610895742018)Acceleration
A final point on the use of proportion metrics: beware of acceleration. If you measure the proportion of users that take some action that they are very likely to take eventually, regardless of the treatment they receive, the likelihood that your proportion metric will show no lift increases as you continue to run your experiment. While you may have lifted the number of times the action was taken or reduced the time to take the action, you won’t have lifted the unique conversions per user in the experiment.
In the following example, we split control and treatment evenly, with identical and deterministic visit conversion. However, we model the first arrival times of these visits as exponential with individual lambdas distributed log-normally. Furthermore, we assume a 10% increase in lambda for members of the treatment.
We see visit conversion take an early lead for the treatment group before converging to what we know a priori are identical long-run conversion rates.
At Faire, this has happened when we’ve tracked the unique conversions to visiting a brand page in the sample of existing retailers. Because most active retailers will visit a brand within a matter of days or weeks, we sometimes see a lift in this metric initially spike and then converge to zero as the experiment matures. These novelty and primacy effects can be pernicious if not detected [3]. That’s not to say that accelerating good behavior isn’t worthwhile. But it is important to understand whether you are lifting metrics or simply speeding them up.
Fewer Metrics
Finally, when it comes to experiment metric selection, less is usually more. As you increase the number of hypotheses you test in your experiment you also increase the likelihood of Type I errors. Depending on your tolerance for making these errors, you will want to control for the family-wise error rate (FWER) or the less-stringent false discovery rate (FDR). FWER techniques, such as the Holm–Bonferroni method, control for the probability of at least one Type I error, while FDR procedures, such as the commonly-used Benjamini–Hochberg procedure, provide weaker guarantees around the expected proportion of incorrectly rejected null hypotheses. Below we demonstrate how in an experiment with ten metrics the use of FDR control reduces the number of significant tests from six down to four. Regardless of the approach you take or the specific method you use, the more comparisons you make via additional metrics the more data you’ll need to reach a significant result.
The same principle applies to the number of variants in your experiment. Tests with more variants test more hypotheses and, all else equal, require more data to reach significance. Ruling out additional treatment variants based on factors such as cost, complexity, or even strong prior beliefs around what will work and what won’t, can be a way to not only design more powerful tests but also cut scope for your Product, Engineering and Design teams. By forcing your team to choose a single primary metric, fewer variants, and as few secondary metrics as absolutely necessary to make a decision you can significantly reduce the time to make decisions and ship product.
Machine Learning
In the next post in this series, we’ll discuss how we use time-boxing, outlier removal, and stratification to reduce metric variance. We’ll then discuss a generalization of stratification known as CUPED, the success we’ve had with this technique using simple linear models, and how it can be generalized using non-linear machine learning approaches. Later posts will cover power analysis, sequential testing, and dynamic traffic allocations strategies for reducing experiment durations.
Acknowledgments
Thank you, Daniele Perito, for your input and guidance.
[0] 2018 Small Business profile
[2] A Dirty Dozen: Twelve Common Metric Interpretation Pitfalls in Online Controlled Experiments
[3] Novelty/Primacy Effect Detection in Randomized Online Controlled Experiments